無限ラダーに隠された黄金比
[2]無限ラダーに隠された黄金比
黄金比というものを知っている人も多いのではないでしょうか。知らない人
のために簡単に述べておきましょう。(黄金比についてここでは述べ切れない程
面白い話があるので興味のある人は文献やインターネットで検索してみてください)
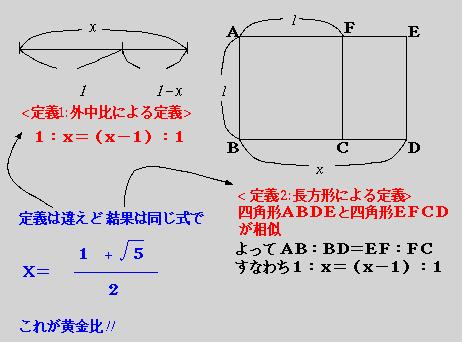
簡単にいうと長方形からその短辺を共通にする正方形を取り去ってのこった長方形
が元の長方形と相似の場合、この長方形の縦横比を黄金比といいます(図参照)。
また、黄金比のことを外中比ともいいます(図左側の定義がわかりやすいでしょう)。
上の図の長方形こそ今から述べる無限ラダーの図式解法になっているのです。
この黄金比を持った長方形は身の回りにたくさんあります。例えばテレホンカード
、名刺等。昔に遡ればパルテノン神殿、ミロのビーナス、ピラミッドにも見受けられ
るのです。昔からこの比が均整のとれた形だとしていろいろな美術品に採用されて
きました。
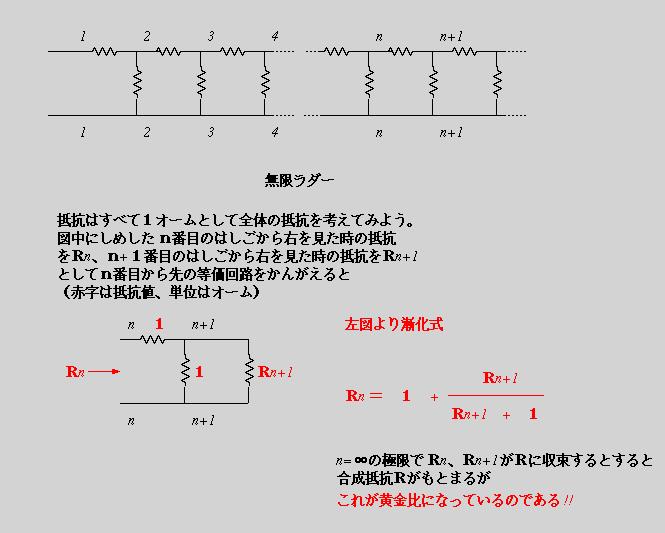
さて、無限ラダーに話を移してみましょう。無限ラダーとは、図に示したように
抵抗が直列、並列、直列、並列.....と無限に続くものをいいます(ラダーとは
ladder=はしごのこと)。図中に示したように漸化式を使って解析的に解くと
全体の合成抵抗は黄金比になっているのです!!
でも解析的に解いてしまうともともと図形と関連の深い黄金比がなぜでてきたのか
わかりません。そう、ここで抵抗回路を図形に変換してやることでこの問題は
解決するのです。
ちなみに黄金比は幾何学と関係なさそうな分野でもでてきます。
しかし、ここでやるように一見関係なさそうな分野が裏でつながっている可能性は
十分あるので黄金比がでてくれば、それが図形とつながっていて幾何学的にその問
題を説明できないかを考えてみると新しい発見があるかもしれません。
ということで無限ラダーの幾何学的解法を考えてみましょう。
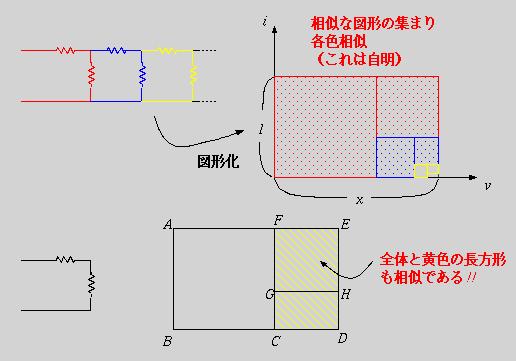
これが無限ラダーの図式表現である。証明したいのは、全体の合成抵抗つまり
図中のxが黄金比になることである(傾きの逆数が抵抗値ということを思い出して
下さい。)また、どの抵抗も1Ωなので1個の抵抗に相当する
図形は正方形である。
ここで大事なのは、抵抗は無限に
同じ形で続くので、どの部分をとっても同じ形をしているということである。
図中に示した赤、青、黄の図形は相似になるし、このような相似の図形が無限に詰
まっているのである。自己相似形の集まりということから黄金比が出てくる
雰囲気が出てきました。もちろんこの相似である事実からxを求めることは簡単に出来
ます。が、四角形ABDEと四角形EFCDが相似であることがわか
れば一番最初に述べた黄金比の定義2そのものになっているため計算なしでこの長
方形は黄金比を持った長方形だとわかってしまうのである。
ここで以前述べた双対の話を思い起こしてもらいたい。無限ラダーは直列並列が交互
に並んでいるため上の話ではその直列並列の二つの抵抗をワンセットにしてその図形
の相似性を述べた。しかし、この直列と並列というのは双対の概念で
本質は同じである。
この双対の概念を図の上で全く同じにしようと思えば
座標自体(電流と電圧も双対の概念!)もひっくり返してやればよいことになる。
つまり、抵抗が直列並列と入れ替わるごとに相似な図形が縦横ひっくり返った
形で出現するはずである。その相似な図形こそ四角形ABDEと四角形EFCDなのである!!
(少しかんがえてみよう!)