電磁対称性を持った回路

京都大学電子工学専攻小林拓真
(浦出芳郎、中田陽介監修)

こんにちは。皆さんは電気回路に馴染みがあるでしょうか。

回路の素子にはコイルやコンデンサがありますが、これらを組み合わせてつくる回路は周波数によってその特性が変わることが知られています。その性質は、たとえば身近なものではラジオの同調回路や、携帯電話の受信機構などに用いられており、日々皆様に親しまれております。

電磁気学的な観点では、コンデンサは電場と、コイルは磁場とそれぞれ密接に関係しておりますが、電磁場の間には不思議な類似性がみられます。中学や高校の授業などで、電気力線や磁力線などを教わって、その類似性に気が付いていた人もいるかもしれませんね。

今回の記事では、電場と磁場の入れ替えに対して対称性をもった回路において起こる、不思議な現象をご紹介いたします。

共振回路

コンデンサやコイルをふくむ単純なRLC回路において、共振と呼ばれる現象が起きます。共振とはこの場合、電源の入力周波数がある一定値となった時に、インピーダンス（交流に対する抵抗のようなもの）が極大（極小）値となることを指します。

例えば図のようなLCの並列２端子回路を考えると、両端のインピーダンスは、\(Z=\frac{\mathrm{j} \omega L}{1-\omega^2 LC}\) (jは虚数)となって、その絶対値は、角周波数が\(\omega=\frac{1}{LC}\)のときに最大値をとります。これはつまり共振時に回路が開放しているようにみなせるということです。

こうした現象は、コンデンサにたまった電気エネルギーとコイルにたまった磁気エネルギーが行き来して振動することで発現します。

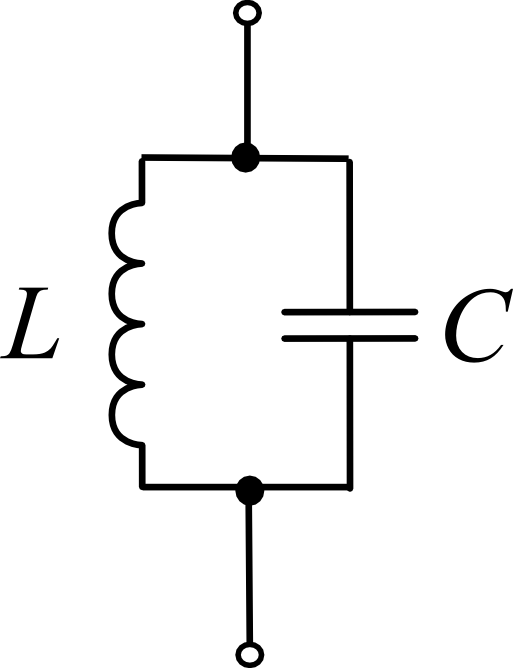
双対回路

ここで、双対という概念が登場します。双対というのは難しいことばのようですが、２つのものの間に“裏返し”の関係があるような場合に使います。このように捉えると、男と女、内と外、歓喜と悲劇、日常のいたるところに双対関係は存在しています。

電気回路にこの双対という考えをあてはめると、ある回路Nの双対回路N’は次のような操作でつくることができます。（ただしここでNは、変圧器を含まないRLC回路を想定しています。）

メッシュを接点でおきかえる
元の枝を横切るように上で出来た接点を結んでいく

ここでメッシュとは、回路中の枝によって隔てられた領域、枝とは接点と接点を結ぶ線です。この操作を図で表すと以下のようになります。

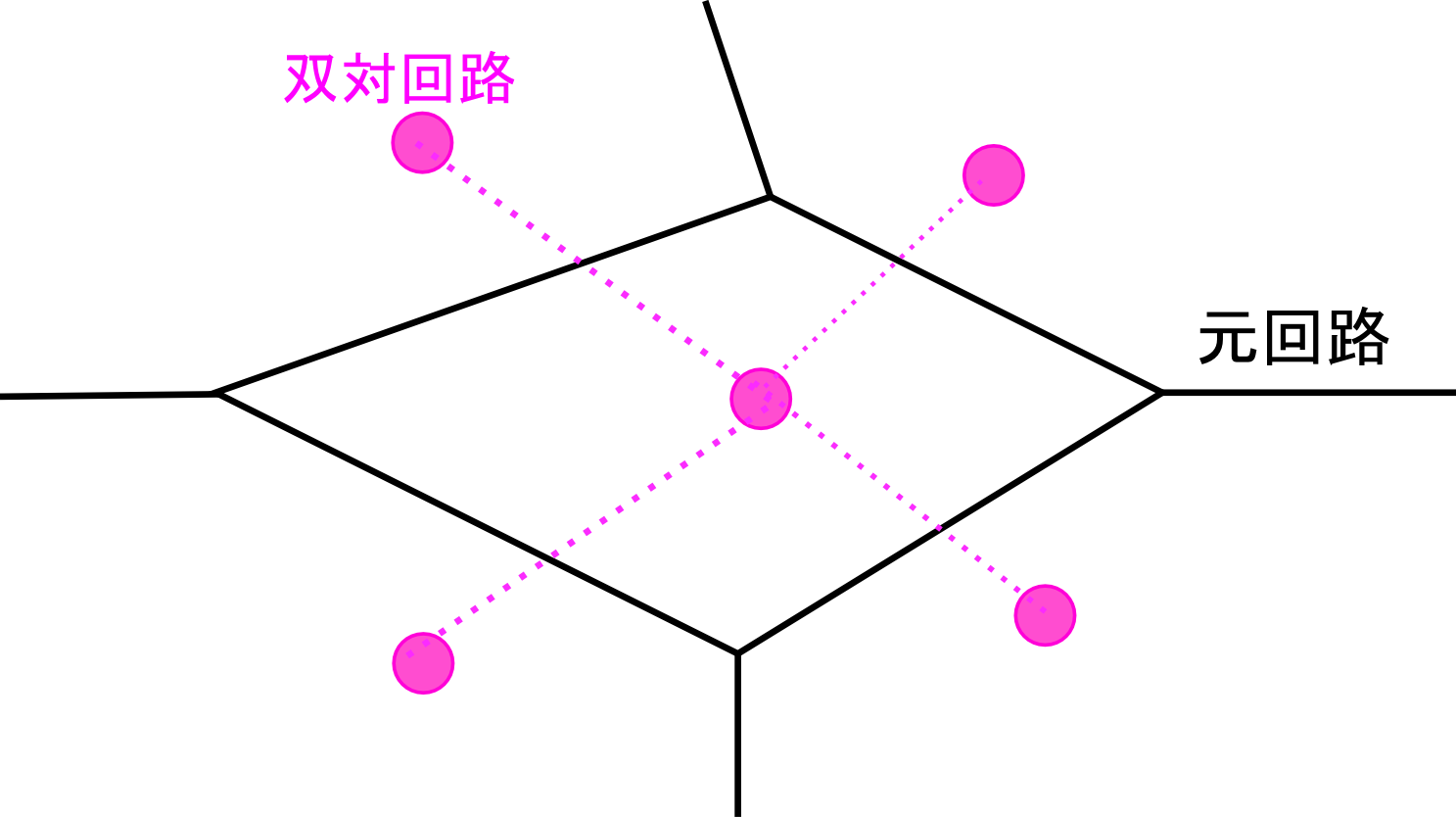
たとえば、2つの抵抗の直列接続と並列接続とは、双対関係にあります。ここで強調しておきたいことは、双対とは”構造上の”裏返しである、ということです。

逆回路

前節では構造上の裏返しについて述べましたが、ここではインピーダンスにとっての裏返しである”逆回路”という考えを導入します。目に見えないからといって身構える必要はありません。逆回路は、以下のように定義されます。

「２つの二端子回路のインピーダンスをそれぞれ \(Z_1,\ Z_2\)とするとき、\(Z_1 Z_2 ={R_0}^2\)ならば２つの回路は\(R_0\)に関して互いに逆回路である」という。

ここで、\(R_0\)に関する逆回路の対応表を以下に示します。インピーダンスの裏返しを考えれば、コイルの反対はコンデンサ、コンデンサの反対はコイルになります。

元回路	⇔	逆回路
抵抗\(R\)	⇔	抵抗\({R_0}^2/R\)
インダクタンス\(L\)	⇔	キャパシタンス\(L/{R_0}^2\)
キャパシタンス\(C\)	⇔	インダクタンス\(C{R_0}^2\)

逆構造（双対回路＋逆回路）

ここで、今までの“双対回路”と“逆回路”を組み合わせたいと思います。つまり、元の構造と比較して構造が裏返っており、全ての素子が\(R_0\)に関して逆回路となっているような構造を、逆構造と呼ぶことにします。逆構造に関してなかなか興味深い定理があるので、それを以下に示します。

「二端子回路Nの抵抗に関する逆構造をN’とする。Nの端子間インピーダンスを\(Z\)、N’の端子間インピーダンスを\(Z'\)とすると \(ZZ'={R_0}^2\)が成り立つ。」・・・(＊)

これは以下の話の根幹となる重要な定理なので、＊マークを付けました。略証はこちら

自己双対回路（逆構造がもとの構造に一致！）

これで準備が整いました。ここからが面白いところです。ある回路Nの抵抗に関する逆構造N’が、N自身に一致するような場合を考えます。Nとは一般的なRLC回路であり、共振回路の節で示したように、そのインピーダンスは入力周波数に依存した共振特性を示すように思われます。

しかし、ここで定理（＊）をじっくりと眺めてみると、逆構造N’がNと一致する場合には当然のように\(Z=Z'\)であり、\(Z^2={R_0}^2\)、つまり\(|Z|=R_0\)となるのです。この結果は、RLC回路Nのインピーダンスの絶対値が、周波数に依存せずに一定値を示すということを表しています。不思議ですね。

以下に自己双対回路の一例である、教科書でおなじみのブリッジ回路を示します。

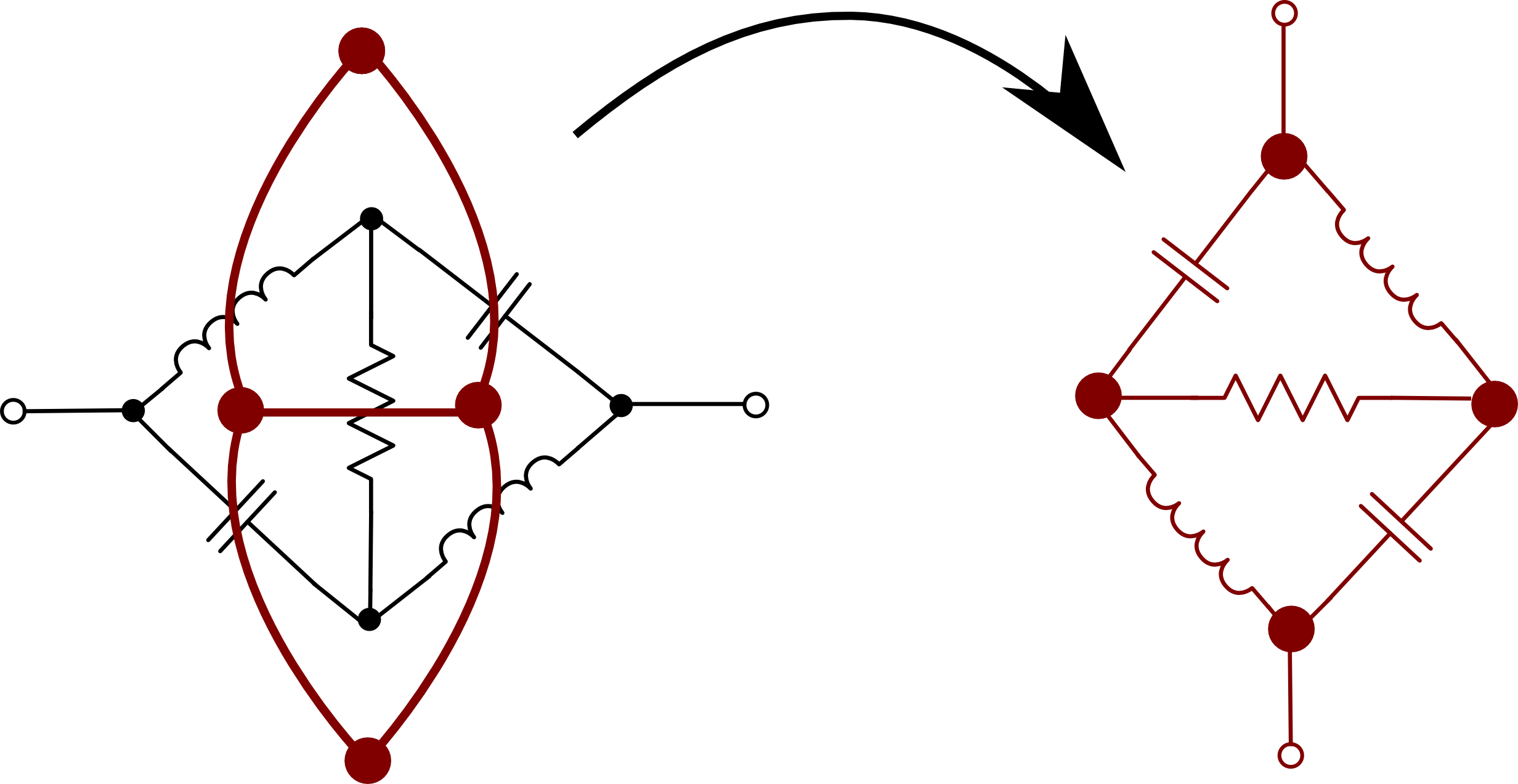
図のように、ブリッジ回路の抵抗\(R_0\)に関する逆構造は、またブリッジ回路になります。 \(R_0=\sqrt{\frac{L}{C}}\)ととれば、コンデンサ\(C\)の裏返しはインダクタ\(C{R_0}^2 =C\frac{L}{C}=L\)となり、インダクタ\(L\)の裏返しは\(\frac{L}{ {R_0}^2}=C\)となります。

真ん中の抵抗を\(R=R_0=\left(\sqrt{\frac{L}{C}}\right)\)と選べば、その裏返しは\(\frac{ {R_0}^2}{R}=R_0\)となるので、両者は完全な自己双対回路となります。すなわちこの時、周波数に依存しないインピーダンスが得られることが予測されます。

実験による検証

ブリッジ回路のインピーダンスは、中央の抵抗を\(R=\sqrt{\frac{L}{C}}\)となるように選べば、周波数無依存になるということが以上の議論によって導かれました。

本節では、これを実験的に検証するため、真ん中の抵抗を可変抵抗として、(1) \(R>\sqrt{\frac{L}{C}}\)　 (2) \(R<\sqrt{\frac{L}{C}}\)　 (3) \(R=\sqrt{\frac{L}{C}}\)　の３パターンでブリッジ回路インピーダンスの絶対値の周波数依存性を調べました。（位相成分については、本議論にあまり関係しないので割愛します。）

\(L=2.2\,\mathrm{mH}\),　\(C=86\,\mathrm{nF}\),　\(r=3.3\,\Omega\)　として、
(1) \(R=205\,\Omega\)　(2) \(R=0.160\,\Omega\)　(3) \(R=161\,\Omega\ \left(\sim \sqrt{\frac{L}{C}}\right)\)　の３パターンでAB間のインピーダンスの周波数依存性を測りました。

ここで強調しておくことは、重要なのは実験回路中央にあるブリッジ回路であり、他の部分は実験の都合上必要となる部分です。

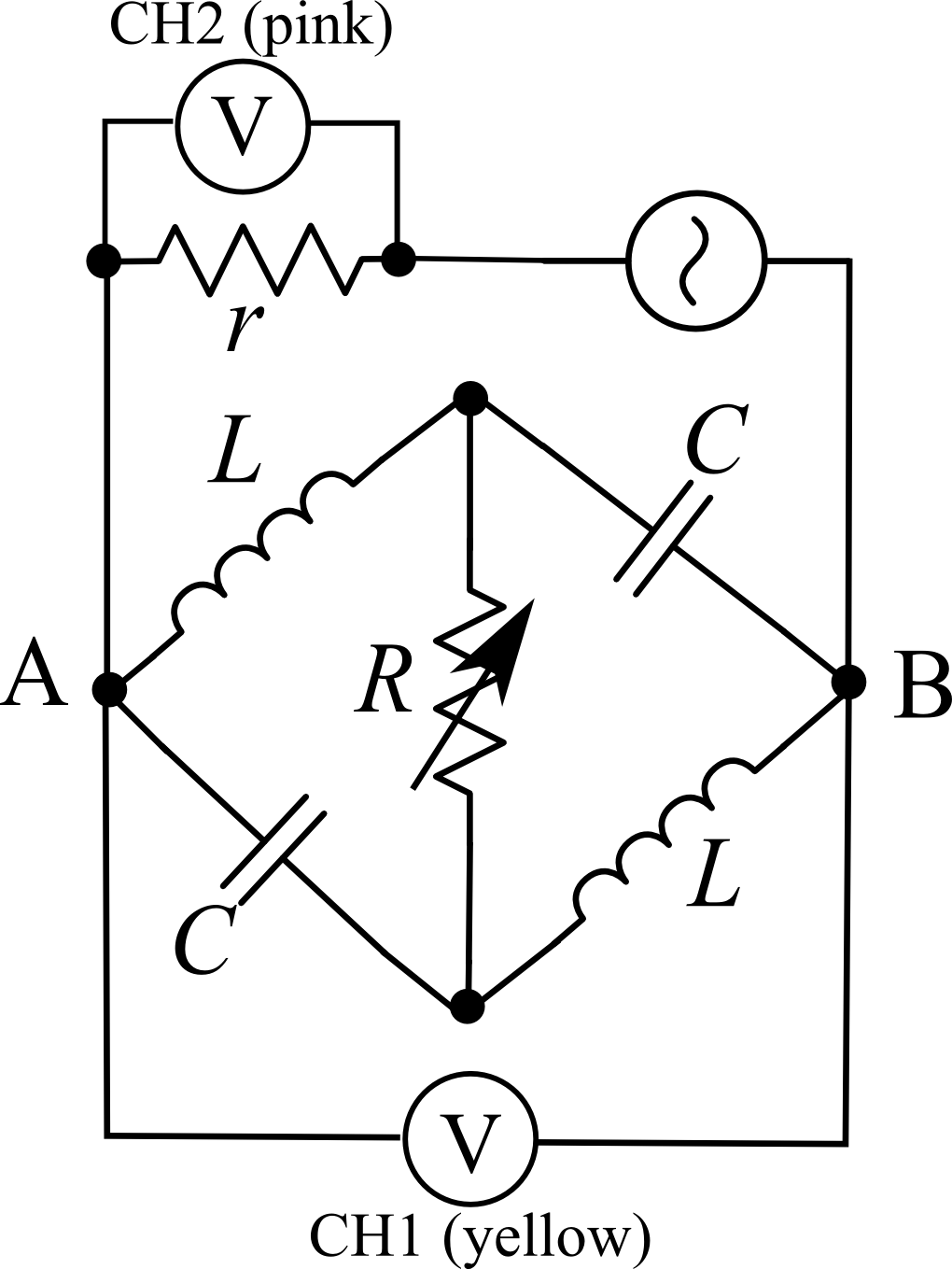
測定に用いた回路。
入力にはファンクションジェネレータ、出力の検出にはオシロスコープを使用。

ここで強調しておくことは、重要なのは実験回路中央にあるブリッジ回路であり、他の部分は実験の都合上必要となる部分です。

まず、実験結果を動画で示します。動画中のオシロに出てくる二つの波形の関係について着目してください。(ピンクと黄色のそれぞれが、 AB間の電流と電圧に対応しています。横軸は時間です。) 画面右側のファンクションジェネレータの周波数を変えながら測定を行なっています。

このように、動画において、(1) (2) の場合は一般にコイルやコンデンサを含んだ回路に現れるように波形の周波数依存性が観察されますが、(3)の場合にはそれが見受けられないことが分かります。以下にブリッジにおけるAB間のインピーダンスの周波数依存性について、その実験のデータを掲載します。

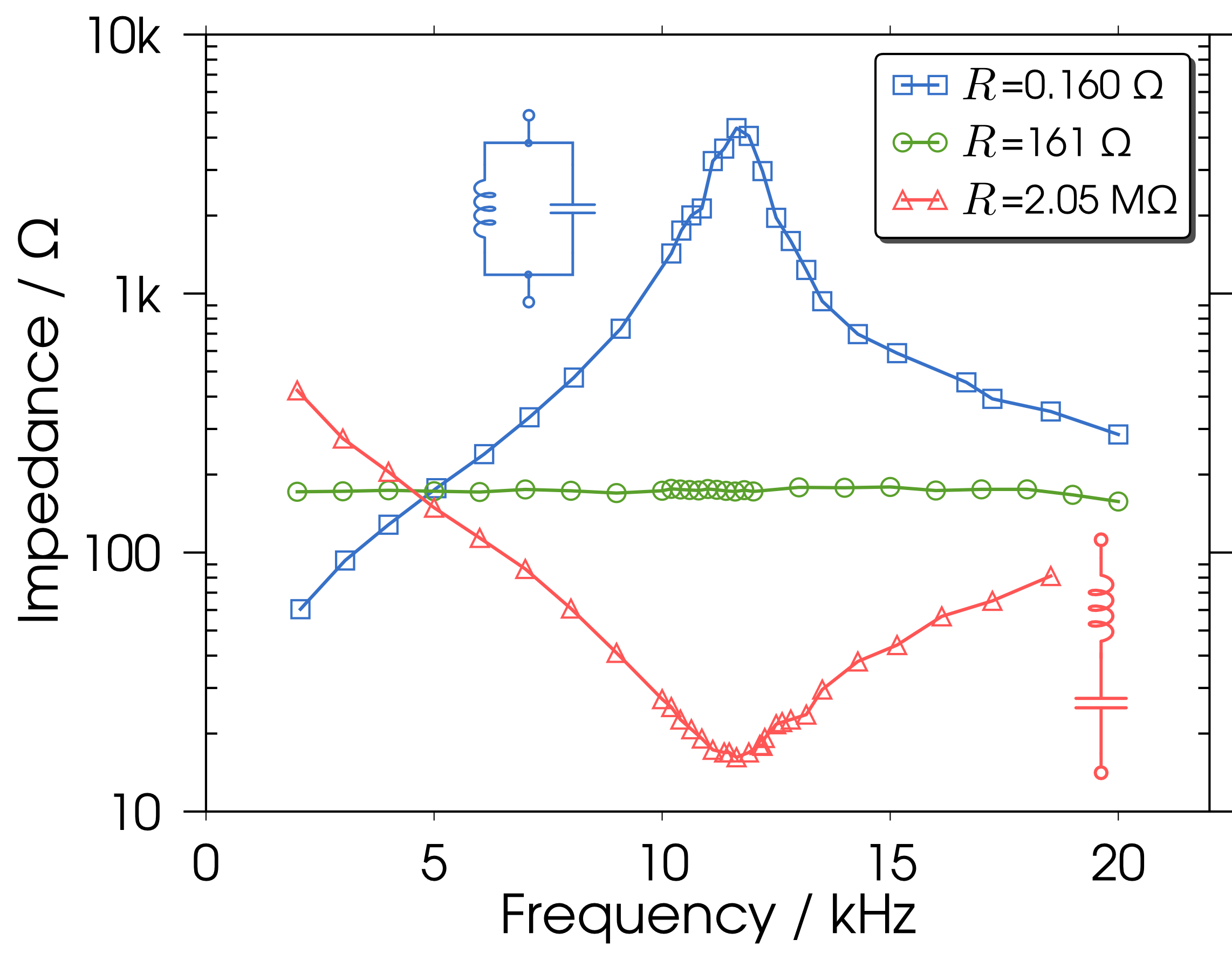
このように(1) (2)の場合は、ブリッジ回路の共振周波数の付近で明瞭な共振特性が観察されていますが、(3)の場合においては周波数に依存しないことが見事、実験的にも確認されました。面白いですね。

まとめ・おまけ

今回一例を挙げたように、インピーダンスが周波数無依存になる（共振しない）ような回路を“定抵抗回路”と呼びます。こういった回路は、たとえばスピーカーの音が周波数ごとに大きくなったり小さくなったりしないように使われています。

上の議論で示されたように、ブリッジ回路が定抵抗回路となり得ることの起源は、どうやらその回路のもつ対称性にあったようです。上手く中央の抵抗を選べば、ブリッジ回路は“ぼくたちの目”にとっても、“電磁場”にとっても対称な構造となることで、定抵抗回路となります。マクスウェル(James Clerk Maxwell) のまとめた数本の式に現れる電場と磁場の間には明瞭な双対関係が見て取れます。

電気回路においても、コイルの裏返しはコンデンサ、コンデンサの裏返しはコイルとなって、それらの間に美しい双対性が現れます。ここにはまるで、白を見れば天使が映り、黒を見れば悪魔の映る、かのエッシャー(Maurits Cornelis Escher) の絵のような感動が潜んでいるように感じられます。ひょっとすると、僕たちの多くが何の疑いもなく芸術に共感し魅了されるのは、それが僕たちの世界を支配する法則に類似しているからなのかもしれません。

最後は小言で飾りましたが、皆さんの知見に少しでも貢献できた、もしくは単純に楽しんで読んでいただけたなら、僕にとっては無上の喜びです。有難うございました。