インクジェットプリンタと
導電性インクで作る
自己双対抵抗膜
京都大学電子工学専攻 岩井亮憲
(浦出芳郎、中田陽介 監修)
身の周りの電子機器が急激に増えている現代において、一人に一つのスマートフォンやノートパソコンはもはや当たり前となり、誰もが電子機器を自在に使いこなして生活しています。そして、これらの便利な機械の中には、とんでもない数の電子パーツが組み込まれ、大きな電子回路となっているのです。つまり、私たちは電子回路まみれ、電子回路だくの状態で生活していることになります。
私は、電子回路がさらに身近になる「導電性インク」を用いて電子回路の趣深い性質「双対性」に関した実験を行ったのでご紹介します。
導電性インク
年賀状を印刷したり、旅の思い出を印刷したりと、プリンターはすっかり家電の仲間入りをしましたが、導電性インクはこのプリンター用の金属インクのことなのです。多少ニッチかもしれませんが、パソコンで描いた通りのパターンと濃淡をそのまま金属のパターンとして印刷できることは大きな魅力です。いろいろな電子機器の中には薄い基板が入っていて、この上にたくさんの電子部品が組み込まれているのですが、この基板をプリンターでお手軽に作成できるようになるかもしれません。
次に、実験の原理を簡単にご説明します。
双対性(回路)
回路には双対回路というものがあり、節点と枝を入れ替えた構造のことを指します。具体的には【図1】を見て下さい。黒色の枝と接点が構成している三角形の回路が元々の回路構成であるとします。このとき、3つの接点と6本の枝が領域を1〜4の4つに分けています。分けられた領域1つにつき1点の節点を与え、これらを繋ぐことによって新たな回路(図の赤色の回路)を構成することができます。この回路が双対回路になります。
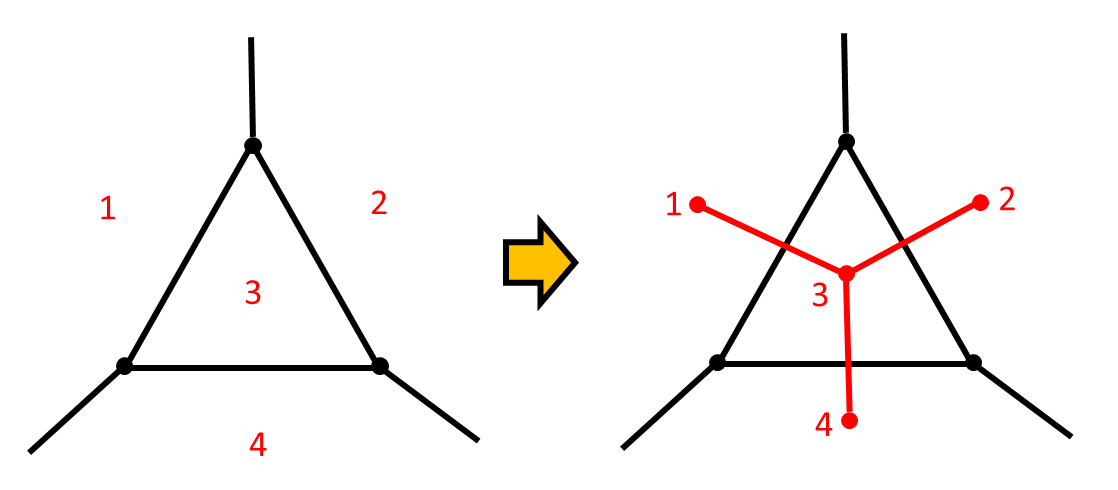

回路には双対回路というものがあり、節点と枝を入れ替えた構造のことを指します。具体的には【図1】を見て下さい。黒色の枝と接点が構成している三角形の回路が元々の回路構成であるとします。このとき、3つの接点と6本の枝が領域を1〜4の4つに分けています。分けられた領域1つにつき1点の節点を与え、これらを繋ぐことによって新たな回路(図の赤色の回路)を構成することができます。この回路が双対回路になります。
次に、この双対回路を具体的なインピーダンスを持った素子を含む回路にあてはめるとどうなるかを見てみます。双対回路の形状の作り方は上で見たとおりです。ここで、素子のインピーダンスは【図2】に示したように、あるインピーダンス\(Z_0\)の2乗を除した値に入れ替えられます。ここで、端子間のインピーダンス\((Z_\mathrm{total},Z'_\mathrm{total})\)の間には、以下の趣深い関係があります。
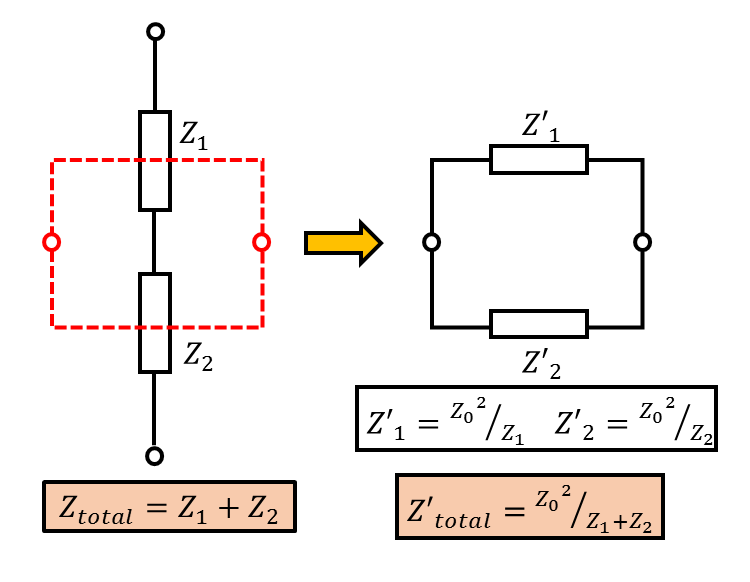
次に、この双対回路を具体的なインピーダンスを持った素子を含む回路にあてはめるとどうなるかを見てみます。双対回路の形状の作り方は上で見たとおりです。

ここで、素子のインピーダンスは【図2】に示したように、あるインピーダンス\(Z_0\)の2乗を除した値に入れ替えられます。ここで、端子間のインピーダンス\((Z_\mathrm{total},Z'_\mathrm{total})\)の間には、以下の趣深い関係があります。
さらに、双対回路のインピーダンスを \(Z'_1=Z_2,Z'_2=Z_1\) と選べば \(Z_0=\sqrt{Z_1 Z_2}\) となります。
では、この双対性を抵抗シートに当てはめるとどのようになるでしょうか。
双対性(抵抗シート)
抵抗シートの場合も、電子回路と同じように考えることができます。抵抗シートが二つのアドミタンス成分 \(Y_1,Y_2\) が平面上に分布することによって構成されているとします。【図3】にあるように、電極を接続した場合の電極間の実効的なアドミタンスを \(Y_\mathrm{eff}\) とします。この値は先ほどの電子回路における端子間のインピーダンスに当たるものです。抵抗シートの場合の双対な構成は、図にあるように電極位置を90度回転し、かつアドミタンス成分を \(Y'_1={Y_0}^2/Y_1, Y'_2={Y_0}^2/Y_2\) と入れ替えたものです。実効的なアドミタンスの間にも、先ほどと全く同様の関係が成り立ちます。
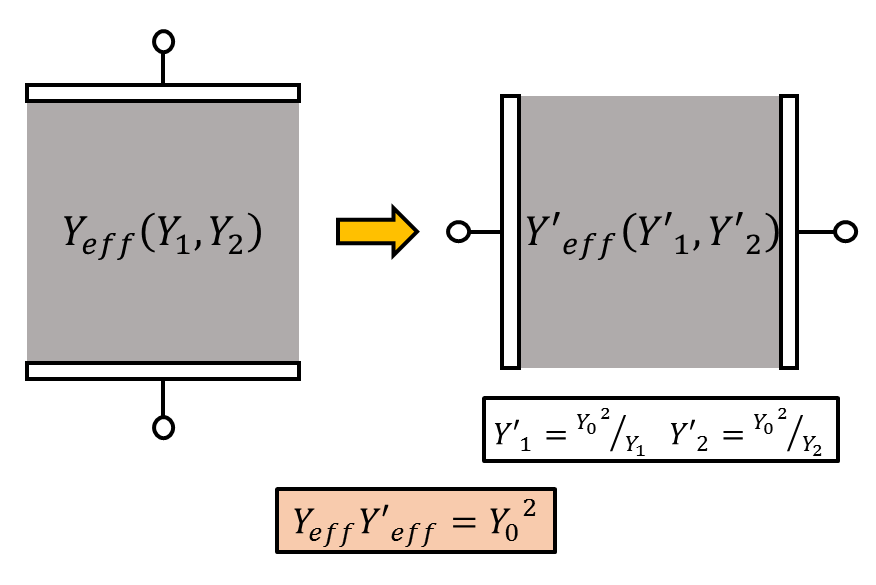

抵抗シートの場合も、電子回路と同じように考えることができます。抵抗シートが二つのアドミタンス成分 \(Y_1,Y_2\) が平面上に分布することによって構成されているとします。【図3】にあるように、電極を接続した場合の電極間の実効的なアドミタンスを \(Y_\mathrm{eff}\) とします。この値は先ほどの電子回路における端子間のインピーダンスに当たるものです。抵抗シートの場合の双対な構成は、図にあるように電極位置を90度回転し、かつアドミタンス成分を \(Y'_1={Y_0}^2/Y_1, Y'_2={Y_0}^2/Y_2\) と入れ替えたものです。実効的なアドミタンスの間にも、先ほどと全く同様の関係が成り立ちます。
さらにここで、双対な構造におけるアドミタンス成分を \(Y'_1=Y_2,Y'_2=Y_1\) とすれば、実効的なアドミタンスは
となります。つまり、ある抵抗シートAとAを90度回転し、かつアドミタンス成分を入れ替えた抵抗シートBの実効的なアドミタンスの積は、構成するアドミタンス成分の積と等しいということになります。
ここから以下のことが導かれます。
「二つのアドミタンス成分で構成された抵抗シートを90度回転し、成分を入れ替えた抵抗シートが元の抵抗シートと一致する(自己双対性がある)場合、その抵抗シートの実効的なアドミタンスは、二つのアドミタンス成分の相乗平均になる」 \[Y_\mathrm{eff}=Y'_\mathrm{eff}=\sqrt{Y_1Y_2}\]
このことを確かめるため、導電性インクを用いてパターンを作成し実験を行いました。
実験
抵抗シート作成のために使用したプリンタ、導電性インクと印刷用紙(基板)は以下の通りです。
- プリンタ:DCP-J740N (ブラザー)
- インク:NBSIJ MU01 (三菱製紙)
- PET基板:NB-TP-3GU100 (三菱製紙)
今回の実験では、次に示す6種類の図形を用意しました。

左の4つの図形(パターン1~4)は、90度回転して成分を入れ替えれば、元の図形に戻る自己双対性を持った図形として用意しました。残りの二つの図形(パターン5、6)は、二つの成分の面積は等しいが、回転すると図形が変わってしまう例として用意しました。
色の濃淡を調節することで、導電性インクを吹き付ける量が変わり、抵抗値が変化します。パターンの両端に付けた黒色の部分は電極です。さらにパターンの隣には、構成している二つの成分のみの正方形を合わせて作成しました。これは、各要素の抵抗値を測定し、その相乗平均とパターンの抵抗値を比較するためです。測定方法はとても簡単で、電極にテスターを接続し抵抗値を測定するだけです。


色の濃淡を調節することで、導電性インクを吹き付ける量が変わり、抵抗値が変化します。パターンの両端に付けた黒色の部分は電極です。さらにパターンの隣には、構成している二つの成分のみの正方形を合わせて作成しました。これは、各要素の抵抗値を測定し、その相乗平均とパターンの抵抗値を比較するためです。測定方法はとても簡単で、電極にテスターを接続し抵抗値を測定するだけです。
それでは実際の測定結果を表で見てみましょう。表の中で二つの成分を \(R_1,R_2\) と表し、実際の測定結果を \(R_\mathrm{de}\) と表しました。
それでは実際の測定結果を表で見てみましょう。
表の中で二つの成分を \(R_1,R_2\) と表し、実際の測定結果を \(R_\mathrm{de}\) と表しました。
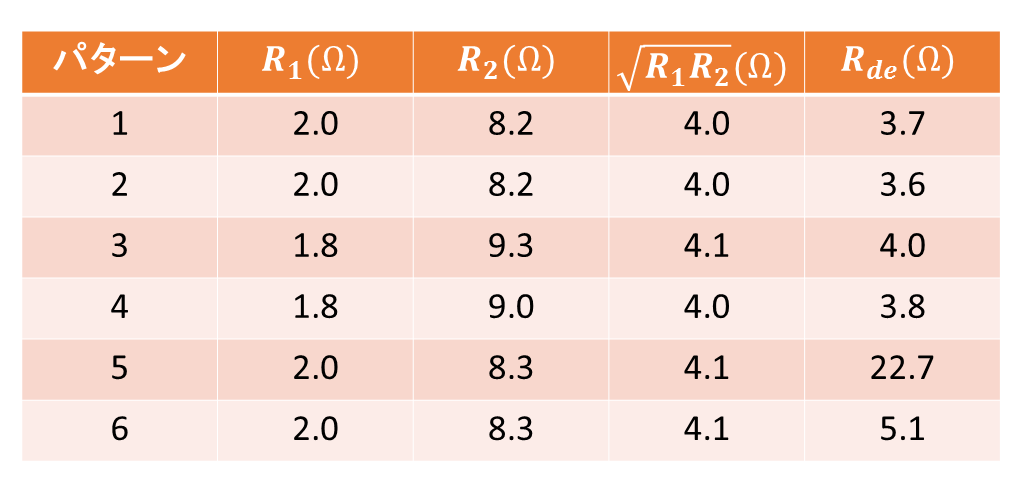
この結果から、自己双対性のある図形においては、測定した抵抗値がおよそ成分の相乗平均になっており、またそうでない図形においては測定した値の方が明らかに大きくなっていることが分かりました。このことから、自己双対性の持つ性質を実験的に確かめることができたとともに、導電性インクを用いて作成した抵抗シートの質の高さをも確認することができました。また、パターン5、6はいずれも測定した抵抗値が相乗平均を超えていることより、自己双対なパターンには、実効的な抵抗値を最小にする性質があるのかもしれません。
結び
抵抗値が低いということは電流にとってはスムーズに流れることができる、つまり移動ができるということだと思います。自己双対な図形は視覚的にもシンメトリーゆえに美しく感じられますが、どうやら電気的にも「美しい」ようです。自然界に数多く存在する対称性(雪の結晶や葉脈に見られるフラクタルetc)なども合理性ゆえに発現した性質ですが、電気の感じている世界も同じなのかもしれません。
参考文献
A. M. Dykhne, Zh. Eksp. Teor. Fiz. 59, 110 (1970) [Sov. Phys. JETP 32, 63 (1971)].
(自己双対抵抗膜の理論に関する論文)
Y. Kawahara et al., Proc. UbiComp 2013, ACM, 363–372 (2013).
(インクジェットプリンタによる導電性インク印刷に関する論文)
