幾何学の難問に電気回路で挑戦
目次
[1] 幾何学的電気回路指南
[2] 無限ラダーに隠された黄金比
[3] 幾何学の難問に電気回路で挑戦
[1] 幾何学的電気回路指南
難問にチャレンジする前に、ここでは抵抗回路を図形に置き換えて考える方法を提示します。電気回路は普通、解析的に扱われることがほとんどで、幾何学と何の接点もないもののように思われます。ところが、幾何学的に扱うことによって非常に多くの情報を盛り込むことができ、違った視点から回路を理解できます。といっても、難しい話ではなくオームの法則さえ知っていれば理解できるので安心して下さい。まず図1を見てみましょう。
オームの法則は周知のとおり、抵抗R、印加電圧V、電流Iとして
I=V/R
だから、電流-電圧特性は図1のように原点を通る傾き1/Rの半直線になる。ここで、印加電圧か電流を決めてやると、動作点が定まり網がけしたような矩形(長方形)が描ける。この矩形の面積が抵抗の消費電力を表しているのも簡単にわかるでしょう。つまり、この矩形を見るだけで、電圧(横幅)、電流(縦幅)、抵抗(対角線の傾き)、消費電力(面積)がわかってしまうのです!!
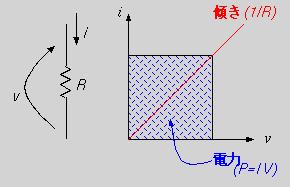
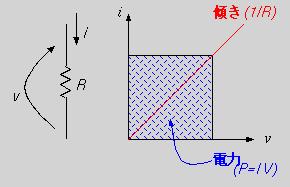
オームの法則は周知のとおり、抵抗R、印加電圧V、電流Iとして
I=V/R
だから、電流-電圧特性は図1のように原点を通る傾き1/Rの半直線になる。ここで、印加電圧か電流を決めてやると、動作点が定まり網がけしたような矩形(長方形)が描ける。この矩形の面積が抵抗の消費電力を表しているのも簡単にわかるでしょう。つまり、この矩形を見るだけで、電圧(横幅)、電流(縦幅)、抵抗(対角線の傾き)、消費電力(面積)がわかってしまうのです!!
その他、電気回路を習っている人には、この図を分析することで、キルヒホッフの電流則-電圧則、抵抗-コンダクタンス、カットセット-タイセット等さまざまな双対の要素が理解できるので、電気回路習得者でも得るところは大きいと思われます。このような専門知識がいるところ(青字で記載)は読みとばしても結構ですが、そんなに難しいことは書いていないので、高校生(あるいはそれ以下でも) 読んでみてください。
最後に注意しなければならないのは、上の図でいえば直線の傾きが1なので抵抗値はその逆数の1Ωと決めつけてしまうことである。これは、電圧電流特性図の1目盛が1V、1Aのときの話で、1目盛1V、1mAならば同じ図でも抵抗値は1kΩである。このように、規格化は自由におこなってよい。次に直列接続と並列接続の場合についてみてみよう。
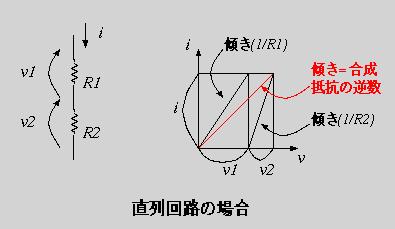
直列接続の場合、2つの抵抗に流れる電流が共通なので、矩形の縦幅は共通である。しかし、電圧は抵抗値に比例して分圧されるので、図2のように矩形が隣に並んだ形になる。そして全体の矩形が合成抵抗についての情報を表している。つまり、その面積が全体の消費電力をあらわし、対角の傾きが合成抵抗の抵抗値の逆数になっている。このことから、直列接続の抵抗の合成式、R=R1+R2、がでてくる。(自分で確かめてみよう!)
並列接続の場合、2つの抵抗にかかる電圧が共通なので、矩形の横幅は共通である。しかし、電流は抵抗値に反比例して分流されるので、図3のように上に矩形が積み上がった形になる。そして全体の矩形が合成抵抗についての情報を表している。つまり、その面積が全体の消費電力をあらわし、対角の傾きが合成抵抗の抵抗値の逆数になっている。このことから、並列接続の抵抗の合成式、1/R=1/R1+1/R2、がでてくる。(これも確かめてみよう!)
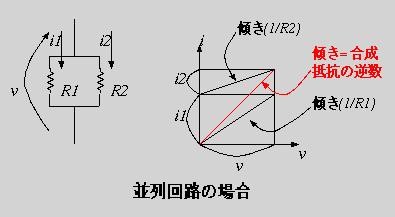

並列接続の場合、2つの抵抗にかかる電圧が共通なので、矩形の横幅は共通である。しかし、電流は抵抗値に反比例して分流されるので、図3のように上に矩形が積み上がった形になる。そして全体の矩形が合成抵抗についての情報を表している。つまり、その面積が全体の消費電力をあらわし、対角の傾きが合成抵抗の抵抗値の逆数になっている。このことから、並列接続の抵抗の合成式、1/R=1/R1+1/R2、がでてくる。(これも確かめてみよう!)
勘のいい人はもう気付いたと思うが、縦と横を入れ換えると直列も並列も同じ構造をしている。これは電圧と電流の関係を入れ換えて(縦と横を入れ換えることに対応)直列並列変換をおこなってやると同じ構造になることを意味している。これは、いわゆる双対変換である!!
もうひとつ、縦と横を入れ換えることで直線の傾きは逆数になる。この傾きは抵抗値そのもので抵抗とコンダクタンス(抵抗の逆数)も双対用語である!! つまり語句を双対な用語で置き換えてやったら同じ図になるのである。
ブリッジについても考えてみよう。
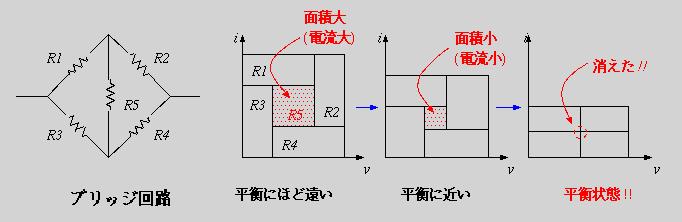
図4のブリッジの両端にある電圧を印加したとき、R1:R2=R3:R4(つまり R1×R4=R2×R3)のときR5の両端の電位差が0になるのでR5に電流は流れない。この状態が平衡状態である。これを今までのように幾何学的に考えてみよう。簡単のためにグラフ1目盛、1V、1Aのときで、初期状態:R1=2Ω、 R2=0.5Ω、R3=0.5Ω、R4=2Ω、R5=1Ωからスタートして、R2とR3を変えることで平衡状態を作ることを考えよう。
初期状態では図4の3つのグラフの一番左(四畳半みたいなやつ)になる。この状態では、R1×R4>R2×R3の非平衡状態でR5に電流が流れている。このことは、図のR5に当たる部分の面積が0でない、つまり電力を消費していることから分かる。だから、平衡状態にするには、この中央部の面積を0にすることを考えればよい。いまは、R2とR3を変えることを考えるので、図のR2とR3に当たる矩形の横の比率を大きくする(抵抗値を上げることで対角線の傾きを小さくしてやる)とよいことが分かる。これは、式の上から考えて平衡状態(R1:R2=R3:R4)にちかづけるためにR2とR3を大きくすることと矛盾しない(当然ではあるが)。平衡条件に近づけていく推移を上図に示している。
平衡状態では、ちゃんとR5に当たる部分が消えてなくなっている。矩形が無くなったから傾きが分からないではないか、と思う人もいるかも知れませんが、R5には電流が流れないのでR5の値はなんでもよく、もっといえば短絡でも開放でもよいことになる。ここでは、2種類の抵抗値を変化させましたが、1種類の抵抗値を変えても平衡状態に変えれるので、この様子を図にしてみるとおもしろい発見があるでしょう。(ドロー系のソフトを活用して作図をしてみるのもいいでしょう。)
以上より分かったことは、抵抗回路は、所詮、今までにあげたような回路の組合せなので、どんな抵抗回路でもそれぞれの抵抗に対応した矩形で敷き詰められた矩形に変換可能だということである。
注意してもらいたいのは、回路全体からなる図形は必ず矩形で、突起やヘコミはなく、そこに敷き詰められた矩形にはすき間が無いということである。逆にいえば、そうなるようにそれぞれの矩形の大きさが(縦横の比は同じまま)変化して前文の条件を満たしてあるのである。
これで題目にあげた難問を、電気回路で実験するために必要な知識は揃いました。ただ、回路を図形に変換するメリットが直接わかる無限ラダーの問題を考えて、より理解を深めてからにしましょう。(はやく実験が知りたい! という人は飛ばしても結構です。)
