幾何学と電気回路

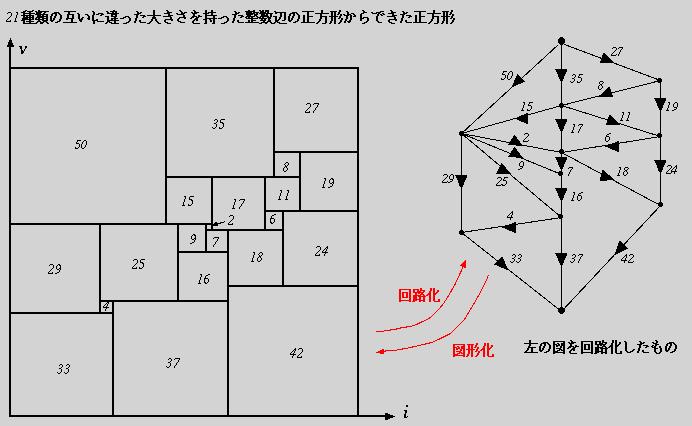
図８を見てみよう。21種類の正方形を敷き詰めて、さらに大きな正方形を構成させた図であり、大切なのは辺の長さが整数で全部違う大きさということです。これは意外と難問で、1978年にコンピューターを使って発見されました。この21個というのが今までの最小のものですので、もっと小さいものを見つけてやろうという人は、チャレンジしてみて下さい。(ちなみに、これより数の多いものは多数発見されていました。)この問題を今までやってきたように回路化して本当にそうなっているかを実験で確かめてみようというのが、最終目標です。

まず気づいて欲しいのは、すべて正方形というのだから、21個の抵抗は全て同じ抵抗(1Ωでなくてもよい。なぜなら座標の規格化を適当に行なってやれば、どんな抵抗でも正方形にできるから)を使うということである。その21個の抵抗(図形化した時の正方形)の直列並列の組合せで上図（図８）の正方形を組立てるのである。その回路が上図（図８）右である。(横が電流、縦が電圧に変わっているのに注意して下さい。深い意味はありません。)
各辺に抵抗1個をおくのですが、図では抵抗の記号を省略しています。ここからは抵抗は1Ωだとして説明すると、回路の端子間に112Vの電圧を加えたとき(左の図の大きな正方形の1辺は112であるから)、正方形の1辺の長さ、例えば50のものに相当する抵抗には50Vの電圧がかかり、50Aの電流が矢印の方向にながれていることになる。

この回路の正しさを理解するためには、2つ確かめるポイントがあります。1つは、上端からスタートして回路を矢印の方向に進んでいって下端に到着する時、通った数字の合計は常に112であるという点である。これはキルヒホッフの電圧則に相当します。もう一つは、ある点に注目して、そこに矢印が向いているものの数字の合計と、ここから出ていく矢印の数字の合計は一緒であるということです。これは、各点に入ってくる電流と出ていく電流の量が等しいというキルヒホッフの電流則に相当します。(上端と下端でそうなっていないのは、図に電源から来る線を描いていないからである。)

こうして出来上がった回路の合成抵抗は、もともとの21個の抵抗の値と同じです。(出来上がった矩形も正方形だから。) これを実験で確かめてみましょう。

実験

まず抵抗を用意しましょう。ここで注意しないといけないのは、抵抗値とかける電圧です。間違っても1Ωの抵抗を使って112Vもかけないで下さい。112A流れることになり非常に危険です。(その前にブレーカーが落ちますが。)電流はmAのオーダーで十分なので、抵抗は1kΩを使い電圧は11.2Vでいいでしょう。

もう一つ重要なのは精度です。抵抗には、最小0.2Vから最大5Vまでかかるものがあるから、結構な精度が要求されます。少し高級な誤差1%の抵抗(といっても抵抗だから知れてますが)を用意しましょう。これを図に従って半田づけすればできあがりです。(図９参照)

合成抵抗を計るだけであったら、テスター等で十分です。その結果が図10です。
左の数字がそれで、998.6Ω(誤差0.1-0.2%)で使った抵抗の精度からして十分な結果が得られました。

合成抵抗を計るだけであったら、テスター等で十分です。その結果が図10です。

左の数字がそれで、998.6Ω(誤差0.1-0.2%)で使った抵抗の精度からして十分な結果が得られました。

さらに理解を深めるため、電源を両端につないで11.2Vの電圧をかけてみよう。各部分の電位差が図に示したとおりになっているでしょうか？例えば50と数字のかいたところには5Vかかっているはずです。

ちなみに図11に示したのが、上の回路の双対のものです。つまり、電圧と電流を読みかえたものに相当します。縦横を入れ換えても正方形では同じことで、抵抗は1kΩになるはずです。

その結果が図12ですが、996.0Ω(誤差0.4%)になりました。これも十分な精度といえるでしょう。

さらにさらに考察を深めてみよう。

正方形の縦のみ通行可能とし、横を通行不可にする (例えば図13の上の図の黒く網がけした部分)。すると回路の両端を結ぶ線が出来る。図にはいっていない電源線をこれに結ぶと、1つ閉ループが出来る。つまり、この通り道はタイセットに対応して、キルヒホッフの電圧則が導かれるのである。

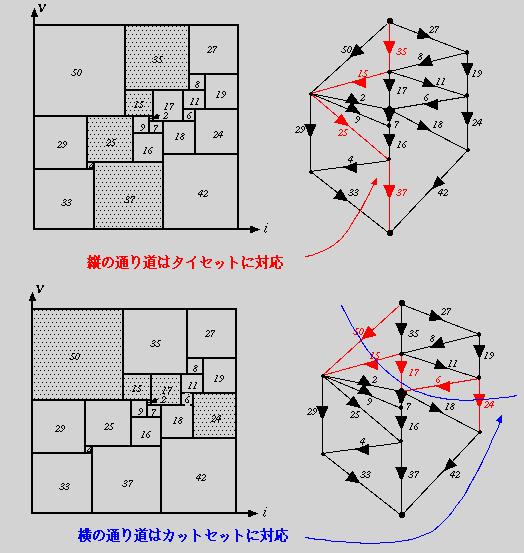
同様に正方形の横のみ通行可能とし、縦を通行不可にする (例えば図13の下の図の黒く網がけした部分)。すると回路が分断される。つまり、この通り道はカットセットに対応し、キルヒホッフの電流則を満足させているのである。また、ここでも縦と横を入れ換えるという双対変換でタイセットとカットセットという双対な概念を導くことが出来たのである。

ほかにもいろいろな通り道を見つけ出すことで、双対な要素が出てくることが考えられます。以上のことから、見方をかえて抵抗回路を幾何学的に考えることが、電気回路初心者にも上級者にも非常に有用だと思っていただけたのではないでしょうか？

参考文献

A.J.W.Duijvestijn,"Simple Perfect Squared Square of Lowest Order"
Journal of Combinatorial Theory,Series B 25,240-243(1978)

M.R.Schroeder
Number Theory in Science and Communication,70-71

公開: 2001-05-13
文責: 中西俊博

目次

[3] 幾何学の難問に電気回路で挑戦

実験

参考文献